Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом. Для облегчения этой работы кафедры физики вузов организуют чтение лекций, практические занятия и лабораторные работы. Поэтому процесс изучения физики состоит из следующих этапов:
1) проработка установочных и обзорных лекций;
2) самостоятельная работа над учебниками и учебными пособиями;
3) выполнение контрольных работ;
4) прохождение лабораторного практикума;
5) сдача зачетов и экзаменов.
При самостоятельной работе над учебным материалом необходимо:
1. Составлять конспект, в котором записывать законы и формулы, выражающие эти законы, определения основных физических пошипи и сущность физических явлений и методов исследования.
2. Изучать курс физики систематически, так как в противном случае материал будет усвоен поверхностно.
3. Пользоваться каким-то одним учебником или учебным пособием (или ограниченным числом пособий), чтобы не утрачивалась логическая связь между отдельными вопросами, по крайней мере внутри какого-то определенного раздела курса.
Контрольные работы позволяют закрепить теоретический материал курса. В процессе изучения физики студент должен выполнить шесть контрольных работ. Решение задач в контрольных работах является проверкой степени усвоения студентом теоретического курса, а рецензии на работу помогают ему доработать и правильно освоить различные разделы курса физики. Перед выполнением контрольной работы студенту необходимо внимательно ознакомиться с примерами решения задач по данной контрольной работе, уравнениями и формулами, а также со справочными материалами, приведенными в конце методических указаний. Прежде чем приступить к решению той или иной задачи, студент должен хорошо понять ее содержание и поставленные в ней вопросы.
Контрольные работы для специальностей, учебными планами которых предусмотрено по курсу общей физики шесть контрольных работ, распределены следующим образом:
1—физические основы механики;
2—молекулярная физика, термодинамика;
3— электростатика, постоянный ток;
4 — электромагнетизм, колебания и волны;
5 — волновая оптика, квантовая природа излучения;
6— элементы атомной и ядерной физики, элементы физики твердого тела.
В данное методическое пособие включены контрольные работы № 1— 6, для этих специальностей.
Контрольные работы для специальностей, учебными планами которых предусмотрено по курсу общей физики пять контрольных работ, распределены следующим образом:
1 — физические основы механики, молекулярной физики, термодинамики;
2 — электростатика, постоянный ток;
3 — электромагнетизм, колебание и волны;
4 — волновая оптика, квантовая природа излучения;
5 — элементы атомной и ядерной физики, элементы физики твердого тела.
Для этих специальностей в первую контрольную работу включены задачи из контрольных работ № 1 и № 2. Они обозначены порядковым номером, заключенным в скобках. Нумерация последующих контрольных работ указана в скобках после номеров работ, приведенных в пособии, т. е. второй контрольной работой для этих специальностей будет работа № 3, поэтому она имеет двойную нумерацию № 3(2); третьей — 4(3); четвертой — 5(4); пятой —6(5).
Каждая контрольная работа для студентов-заочников технологических специальностей включает семь задач, для студентов-заочников инженерно-экономических специальностей — первые шесть задач из соответствующего варианта. Определение варианта задания проводится по единой для всех шести контрольных работ таблице вариантов в соответствии с последней цифрой шифра. Если, например, последняя цифра шифра студента-технолога 7, то в каждой контрольной работе он решает задачи 7, 17, 27, 37, 47, 57 и 67. Студент-экономист, имеющий тот же шифр, решает те же задачи, исключив 67.
Таблица вариантов
|
Вариант |
Номер задач в каждой контрольной работе |
||||||
|
1 2 3 4 5 6 7 8 9 10 |
1 2 3 4 5 6 7 8 9 10 |
11 12 13 14 15 16 17 18 19 20 |
21 22 23 24 25 26 27 28 29 30 |
31 32 33 34 35 36 37 38 39 40 |
41 42 43 44 45 46 47 48 49 50 |
51 52 53 54 55 56 57 58 59 60 |
61 62 63 64 65 66 67 68 69 70 |
УЧЕБНЫЕ МАТЕРИАЛЫ ПО РАЗДЕЛАМ КУРСА ФИЗИКИ
I.ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
ПОЯСНЕНИЯ К РАБОЧЕЙ ПРОГРАММЕ
Изучать основы классической механики надо исходя из представлений современной физики, в которой основные понятия классической механики не утратили своего значения, а лишь получили дальнейшее развитие, обобщение и критическую оценку с точки зрения их применения. Следует помнить, что механика — это наука о простейших формах, движения материальных тел и происходящих при этом взаимодействиях между телами. Движение всегда существует в пространстве и во времени. Диалектический материализм учит, что пространство и время являются основными формами существования материи. Предметом классической механики является движение макроскопических материальных тел, совершаемое со скоростями, малыми по сравнению со скоростью света в вакууме. Движение частиц со скоростями порядка скорости света рассматривается в теории относительности, а движение микрочастиц изучается в квантовой механике.
Контрольная работа № 1 построена таким образом, что она дает возможность проверить знания студентов по ключевым вопросам классической механики и элементам специальной теории относительности. Решая задачи по кинематике, в которых необходимо использовать математический аппарат дифференциального и интегрального исчисления, студент должен научиться определять мгновенные скорость и ускорение по заданной зависимости координаты от времени и решать обратные задачи.
Задачи на динамику материальной точки и поступательного движения твердого тела охватывают такие вопросы, как закон движения центра масс механической системы, закон сохранения количества движения, работа силы и ее выражение через криволинейный интеграл, связь кинетической энергии механической системы с работой сил, приложенных к этой системе, закон сохранения механической энергии. Тщательного изучения и понимания требуют вопросы о поле как форме материи, осуществляющей взаимодействие между частицами вещества или телами, о потенциальной энергии материальной точки во внешнем поле и потенциальной энергии механической системы. Эти вопросы рассматриваются в задачах на примере гравитационного поля.
В задачах на кинематику и динамику вращательного движения твердого тела главное внимание уделялось изучению соотношений между линейными и угловыми характеристиками, понятий момента силы, момента инерции тела, законов сохранения количества движения, момента- количества движения и механической энергии.
В контрольную работу включены задачи по элементам специальной теории относительности, которые охватывают следующие вопросы; относительность одновременности, длин и промежутков времени, релятивистский закон сложения скоростей, зависимость релятивистской массы от скорости, соотношение между релятивистской массой и полной энергией. Решая эти задачи, студент должен усвоить, что законы классической механики имеют границу применимости и что они получаются как следствие теории относительности с->∞.
Задачи в контрольной работе расположены приблизительно в том порядке, в каком соответствующие вопросы рассматриваются в рабочей программе.
Основные законы и формулы
Скорость мгновенная

Ускорение:
мгновенное 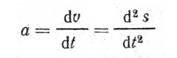
тангенциальное 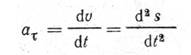
нормальное ![]()
полное ![]()
Скорость угловая
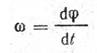
То же, для равномерного вращательного
движения ![]()
Ускорение угловое
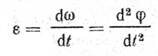
Уравнения равнопеременного
вращательного движения ![]()
Связь между линейными и угловыми величинами, характеризующими движение точки по окружности
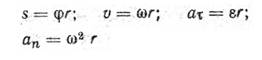
Второй закон Ньютона для поступательного
движения 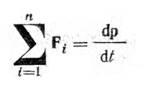
Сила, действующая на тело массы
m (m=const)
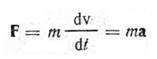
Количество движения материальной точки массы т, движущейся со скоростью v
![]()
Сила, действующая на тело, движущееся по окружности радиуса r
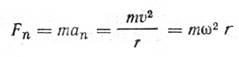
Закон сохранения количества движения для изолированной системы
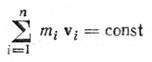
Сила трения (скольжения)
![]()
Скорости шаров массами m1 и m2 после абсолютно упругого центрального удара
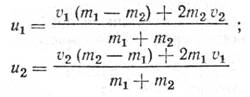
Скорость шаров массами m1 и m2 после абсолютного неупругого удара

Работа переменной силы на
пути s ![]()
Мощность
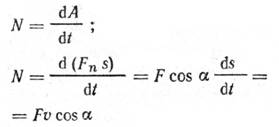
Сила упругости ![]()
Сила гравитационного взаимодействия
![]()
Потенциальная энергия:
упругодеформированного тела
(работа упругой силы) ![]()
гравитационного взаимодействия тела, находящегося в однородном поле тяжести
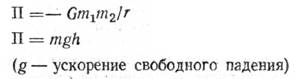
Кинетическая энергия тела
![]()
Закон сохранения механической
энергии ![]()
Напряженность гравитационного
поля Земли ![]()
Потенциал гравитационного
ноля Земли ![]()
Момент инерции материальной
точки ![]()
Моменты инерции некоторых тел массой т:
полого и сплошного цилиндров
(или диска) радиуса R относительно оси вращения, совпадающей с осью цилиндра ![]()
шара радиуса R относительно оси вращения, проходящей через центр масс шара
![]()
тонкого стержня длиной l, если ось вращения перпендикулярна стержню и проходит через центр масс стержня
![]()
то же, но ось вращения
проходит через один из концов стержня ![]()
тела относительно произвольной
оси (теорема Штейнера) ![]()
Момент силы относительно оси
вращения ![]()
Основное
уравнение динамики вращательного движения 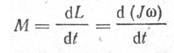
То же, при J=const ![]()
Закон сохранения момента количества движения для изолированной системы
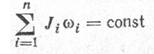
Кинетическая энергия вращающегося
тела ![]()
Работа при вращательном
движении ![]()
Энергия покоя частицы
![]()
Теорема сложения скоростей в
теории относительности ![]()
Зависимость массы частицы от скорости V, сравнимой со скоростью света
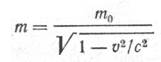
Полная энергия частицы, движущейся со скоростью V, сравнимой со скоростью света
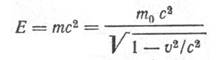
Кинетическая энергия релятивистской частицы
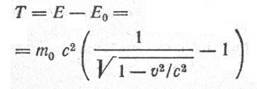
Зависимость длины тела и времени от скорости в релятивистской механике
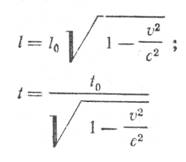
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Движение тела массой 1 кг задано уравнением s=6t3+3t+2. Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды.
Решение. Мгновенную скорость находим как производную от пути по времени:
v = ds/dt; v = 18t3+3.
Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени:
a = dv/dt=d2s/dt2 ; a = 36t.
Сила, действующая на тело, определяется по второму закону Ньютона: F=та, где a согласно условию задачи — ускорение в конце второй секунды. Тогда
F = m*36t; F= 1 кг*36*2 м/с2 = 72 Н.
Ответ: v = 18t2+3; а = 36t; F = 72 Н.
2. Стержень длиной 1 м движется мимо наблюдателя со скоростью 0,8 с. Какой покажется наблюдателю его длина?
Дано: l0=1 м, v = 0,8 с.
Найти l.
Решение. Зависимость длины тела от скорости в релятивистской
механике выражается формулой
![]() , где l0—
длина
, где l0—
длина
покоящегося стержня; v — скорость его движения; с— скорость
света в вакууме. Подставляя в формулу (1) числовые значения,
имеем
![]()
Ответ: l = 0,6 м.
3. Две частицы движутся навстречу друг другу со скоростями: 1) v=0,5 с и и =0,75 с; 2) v = с и u=0,75 с. Найти их относительную скорость в первом и втором случаях. Дано: 1) v=0,5 с, u=0,75 с; 2) v = с, u=0,75 с.
Найти: и1', и2' .
Решение. Согласно теореме сложения скоростей в теории относительности
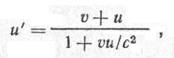
где v, и — скорости соответственно первой и второй частиц; и' — их относительная скорость; с— скорость света в вакууме. Для первого и второго случаев находим:
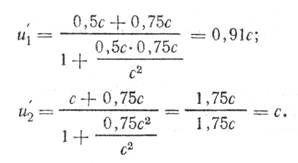
Это значит: во-первых, ни в какой инерциальной системе отсчета скорость процесса не может превзойти скорость света; во-вторых, скорость распространения света в вакууме абсолютна.
Ответ: и1' =0,91 с; и2'=с.
4. На двух шнурах одинаковой длины, равной 0,8 м, подвешены два свинцовых шара массами 0,5 и 1 кг (рис. 1). Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол а=60°, и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и п. упругим. Определить энергию, израсходованную на деформацию шаров при ударе.
Дано: m1 = 0,5 кг, т2=1 кг, а=60°; l=0,8 м.
Найти: H1, ∆Eд .
Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью v. Закон сохранения количества движения при этом ударе имеет вид т1v1 + т2v2= (т1 + m2)v . (1)
Здесь v1 и v2 — скорости шаров до удара. Скорость большого шара до удара равна нулю (v2 = 0). Скорость меньшего шара найдем, используя закон сохранения энергии. При отклонении меньшего шара на угол a (см. рис. 1) ему сообщается
потенциальная энергия, которая затем переходит в кинетическую: т1gh = m1v12/2.
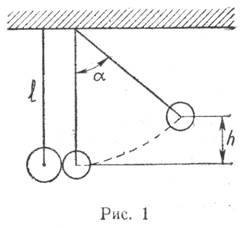
Из рисунка видно, что h1 = l (1- cos a)=2l sin2(a/2), поэтому
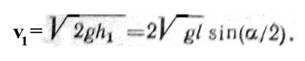 (2)
(2)
Из уравнений (1) и (2) находим скорость шаров после удара:
V=m1v1/( т1+т2)=2 т1![]() sin (α/2)/(т1+т2). (3)
sin (α/2)/(т1+т2). (3)
Кинетическая энергия, которой обладают шары после удара, переходит в потенциальную: ( т1+т2)v2/2= ( т1+т2)gh, (4) где h — высота поднятия шаров после столкновения. Из формулы (4) находим h=v2/(2g), или с учетом (3)
h = 2т12 l sin2 (α/2)/(т1+т2)2;
h = 2(0,5 кг)2*0,8 м*0,25/(0,5 кг + 1 кг)2 = 0,044 м.
При неупругом ударе шаров часть энергии расходуется на их деформацию. Энергия деформации определяется разностью кинетических энергий до и после удара: ∆Eд=1/2m1v12-1/2(т1+т2)v2. Используя уравнения (2) и (3), получаем
∆Eд=2glm1(1- m1/( т1+т2))sin2 (α/2);
∆Eд = 2*9,81 м/с2*0,8 м*0,5 кг(1—0 5 кг/1,5кг)*0,25 = 1,3 Дж.
Ответ: h=0,044 м, ∆Eд =1,3 Дж.
5. Молот массой 70 кг падает с высоты 5 м и ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием 1330 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на деформацию изделия. Систему молот—изделие—наковальня считать замкнутой.
Дано: т1 = 70 кг, h=5 м, ш2=1330 кг.
Найти Ед.
Решение. По условию задачи система молот—изделие—наковальня считается замкнутой, а удар неупругий. На основании закона сохранения энергии можно считать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии системы до и после удара.
Считаем, что во время удара изменяется только кинетическая энергия тел, т. е. незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда для энергии деформации изделия имеем
Едеф= 1 /2m1 v2 - 1 /2 (т1+т2) v'2, (1)
Где v — скорость
молота в конце падения с высоты h; v' — общая скорость всех тел системы после неупругого удара.
Скорость молота в конце падения с высоты h определяется без учета сопротивления воздуха и трения по формуле v=![]() (2)
(2)
Общую скорость всех тел системы после неупругого удара найдем, применив закон сохранения количества движения
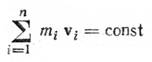 (3)
(3)
Для рассматриваемой системы закон сохранения количества движения имеет вид т1v=(т1+т2)v', откуда v' = т1/(т1 + т2). (4) Подставив в формулу (1) выражения (2) и (4), получим
Ед =m1gh (m2/(m1+m2));
Ед = 70 кг*98 м/с2*5 м * (1330 кг/(1330 кг + 70 кг))= 325,85 Дж.
Ответ: Ед = 325,85 Дж.
6. Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени задана уравнением s = 2t2 +4t+1. Определить работу силы за 10 с с начала ее действия и зависимость кинетической энергии от времени.
Дано: m=1 кг, s = 2t2 +4t+1.
Найти: A, T = f(Т).
Решение. Работа,
совершаемая силой, выражается через криволинейный интеграл А=![]() (1).
Сила, действующая на тело, по второму закону Ньютона равна F=та или F=т(d2s/dt2) (2).
Мгновенное значение ускорения определяется первой производной от скорости по
времени или второй производной от пути по времени.
(1).
Сила, действующая на тело, по второму закону Ньютона равна F=та или F=т(d2s/dt2) (2).
Мгновенное значение ускорения определяется первой производной от скорости по
времени или второй производной от пути по времени.
В соответствии с этим находим
V=ds/dt= 4t+4; (3) a=d2s/dt2=4 м/с2. (4)
Тогда F = т (d2s/dt2) =4m. (5) Из выражения (3) определим ds: ds=(4t+4)dt. (6) Подставив (5) и (6) в уравнение (1), получим
А = ![]() .
.
По этой формуле определим работу, совершаемую силой за 10 с начала ее действия:
А= ![]() = 1
(8*100 + 16*10) Дж = 960 Дж.
= 1
(8*100 + 16*10) Дж = 960 Дж.
Кинетическая энергия определяется по формуле T=mv2/2. (7)
Подставляя (3) в (7), имеем
T = т (4t + 4)2/2 = т (16t2 + 32t + 16)/2 = m (8t2 + 16t + 8) .
Ответ: A= 960 Дж, T = m (8t2+16t+8).
7. Протон движется со скоростью 0,7 с (с — скорость света). Найти количество движения и кинетическую энергию протона:
Дано: v=0,7 с.
Найти: р,Т.
Решение. Количество движения протона определяется по формуле p = mv. (1) Так как скорость протона сравнима со скоростью света, то необходимо учесть зависимость массы от скорости, воспользовавшись релятивистским выражением для массы:
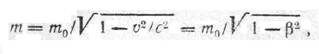 (2)
(2)
где m — масса движущегося протона; m0=1,67-10-27 кг —масса покоя протона; v—скорость движения протона; еc=3-108 м/с — скорость света в вакууме; v/с = β — скорость протона, выраженная в долях скорости света.
Подставляя уравнение (2) в (1) и учитывая, что v =βс, получаем
p = m0cβ![]() ;
;
p = 1,67.10-27 кг*(3*108 м/с)2*0.7/((1-β2)1/2) = 4,91.10-19 кг*м/с. В релятивистской механике кинетическая энергия частицы определяется как разность между полной энергией Е и энергией покоя Е0 этой частицы: T = E-Eo (3) , где Е=m0c2/(1-β2)1/2 ; Eo= m0c2 .
Вычислим энергию покоя протона
Е0= 1,67*10-27 кг*(3*108 м/с)2 = 1,5*10-10 Дж.
Тогда [см. (3)]
T = m0c2(1/(1-0,72)1/2 - 1);
Т =1,5*10-10 Дж (l/(1-0,72)1/2 - 1) = 0,6*10-10 Дж.
Ответ: p=4,91*10-19 кг*м/с, Т= 0,6*10-10 Дж.
8. Какую скорость нужно сообщить ракете, чтобы она, стартовав с Земли, не вернулась на Землю? Сопротивление атмосферы не учитывать.
Дано: R3 =6,37- 106 м; g=9,8 м/с2; R->∞.
Найти vo.
Решение. С удалением ракеты от Земли будет увеличиваться ее потенциальная энергия и уменьшаться кинетическая. По закону сохранения энергии,
mvo2/2 - mv2/2= m(GM/R3 – GM/К) (1)
где ь— масса ракеты; М — масса Земли; G — гравитационная постоянная; v0 и v — скорости ракеты относительно Земли в начальный и рассматриваемый моменты; R3 и R — расстояния от центра Мили до ракеты в начальный и рассматриваемый моменты; GM/R— Потенциал гравитационного поля Земли на расстоянии R от ее центра.
После преобразования уравнения (1) имеем v o2 - v 2= 2GM(1/R3 —1/R). Ракета не вернется на Землю, если ее скорость v будет в бесконечности равна нулю, т. е. v=0 при R->∞. В этом случае vo2=2GM/R3 . (2)
Из закона всемирного тяготения следует, что на поверхности Земли GmM/R32 =mg, откуда GM=gR32 (3) , где g — ускорение свободного падения на поверхности Земли. Подставляя формулу (2) и (3), находим
v02 = 2gR3 , или v0 = (2gR3)1/2
Считая, что ракета приобретает нужную скорость v0 уже вблизи поверхности Земли, находим
![]()
Такая скорость необходима для преодоления гравитационного поля Земли. Она называется второй космической или параболической скоростью.
Ответ: v0=11,2 км/с.
9. Тело брошено вверх с высоты 12 м под углом 30° к горизонту с начальной скоростью 12 м/с. Определить продолжительность полета тела до точек А и В (рис. 2), максимальную высоту, на которую поднимается тело, и дальность полета тела. Сопротивление воздуха не учитывать.
Дано: Н =12 м, φ=30°, v0=12 м/с.
Найти: tа , tb , ymax, xmах.
Решение. В обозначенной на рис. 2 системе координат проекции начальной скорости будут vox = vo cos φ, (1) voy = vo sin φ (2)

Координаты тела с течением времени изменяются в соответствии с уравнением для
равнопеременного движения:
y = H + vot sin φ – gt2/2; (3)
x = vot cos φ . (4)
Время подъема тела найдем из условия, что в наивысшей точке подъема тела его скорость vy=vo sin φ - gt=0 . (2`)
Тогда tпод = vo sin φ/g (5). Время спуска тела от точки С до точки А равно времени подъема, поэтому продолжительность полета тела от точки О1 до точки А равна = vo sin φ/g (5). Время спуска тела от точки С до точки А равно времени подъема, поэтому продолжительность полета тела от точки О1 до точки А равна
tА =2tпод=2v0 sin φ/g. (6)
Максимальную высоту подъема найдем из уравнения (3), подставив в него время подъема из уравнения (5):
ymax=Н +vo2sin2 φ/(2g). (7)
Время полета тела до точки В найдем из уравнения (3), приравняв координату у нулю (y = 0):
tB = v0sin φ/g +((v()sin φ/g )2 + 2H/g)1/2 . (8)
Дальность полета найдем из уравнения (4), подставив в него время движения из уравнения (8):
xmax= votBcos φ . (9)
Тогда [ см. (6)-(9) ]
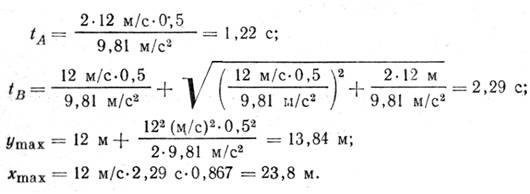
Ответ: tA = 1,22 с, tB = 2,29 с, ymax = 13,84 м, хmaх=23,8 м.
10. По условию задачи 9 найти в момент приземления тела следующие величины: скорость и угол падения тела, тангенциальное и нормальное ускорения тела, радиус кривизны траектории.
Дано: H=12 м, φ=30°, v0=12 м/с.
Найти: vb, β, at, an, R.
Решение. Результирующая, или мгновенная, скорость в точке В (рис. 2, 3)
![]() . Проекцию скорости vy в точке В найдем из уравнения (2') задачи (9), подставив в
него время движения tB [см. (8)]:
. Проекцию скорости vy в точке В найдем из уравнения (2') задачи (9), подставив в
него время движения tB [см. (8)]:

vb =( (122 + 2*9.81*12) м2/с2)1/2 =19,5 м/с.
Из рис. 3 определим угол Р, образуемый вектором скорости vb с осью Ох:
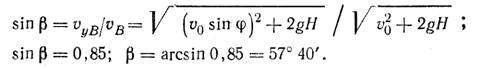
Построим в точке В «треугольник ускорений». Вектор тангенциального ускорения aт направлен вдоль вектора мгновенной скорости в данной точке, т. е. по касательной к траектории; вектор нормального ускорения an перпендикулярен вектору мгновенной скорости vB. Из рис. 3 видно, что
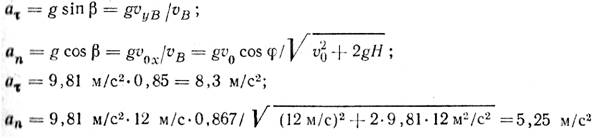
Радиус кривизны траектории в точке приземления определяем из уравнения an=vB2 /R. Имеем
R = =vB2 / an ;
R = 19,52 м2/с2/5,25 м/с2 = 72,5 м.
Ответ: vв=19,5 м/с, β=57°40', ат=8,3 м/с2, an = 5,25 м/с2, R=72,5 м.
11. Тонкий стержень массой 300 г и длиной 50 см вращается с угловой скоростью 10 с-1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Найти угловую скорость, если в процессе вращения в той же плоскости стержень переместится так, что ось вращения пройдет через конец стержня.
Дано: m=300 г=0,3 кг, l=50 см = 0,5м, ω1= 10с-1.
Найти: ω2 .
Решение. Используем закон сохранения момента количества движения
![]() Ji ωi = const (1) , где Ji — момент инерции стержня относительно оси вращения.
Ji ωi = const (1) , где Ji — момент инерции стержня относительно оси вращения.
Для изолированной системы тел векторная сумма моментов количества движения остается постоянной. В данной задаче вследствие того, что распределение массы стержня относительно оси вращения изменяется, момент инерции стержня также изменится. В соответствии с (1) запишем J0 ω1 = J2 ω2 (2)
Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен J0=ml2/12. (3) По теореме Штейнера, J = Jo+md2 , где J — момент инерции тела относительно произвольной оси вращения; J0 — момент инерции относительно параллельной оси, проходящей через центр масс; d — расстояние от центра масс до выбранной оси вращения.
Найдем момент инерции относительно оси, проходящей через его конец и перпендикулярной стержню: J2=Jo + md2; J2=ml2/12+m(l/2)2=ml2/3. (4)
Подставим формулы (3) и (4) в (2): ml2ω1/12= ml2ω2/3, откуда
ω2 = ω1/4, ω2= 10с-1/4 ==2,5с-1.
Ответ: ω2=2,5 с-1.
12. Маховик массой 4 кг свободно вращается с частотой 720 мин-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.
Дано: ω = 0, m = 4 кг, n = 720 мин-1 = 12 с-1; ∆t= 30 с, R = 0,4 м.
Найти: М, N.
Решение. Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения: J∆ ω = M∆t (1), где J — момент инерции маховика относительно оси, проходящей через центр масс; ∆ ω — изменение угловой скорости за промежуток времени ∆t.
По
условию задачи, ∆ω
= - ω0,
где ω0 — начальная угловая скорость, так как
конечная угловая скорость ω = 0. Выразим начальную угловую скорость через
частоту вращения маховика, тогда ω0=2![]() n
и
∆ω=
n
и
∆ω=![]() n.
Момент
инерции маховика J=mR2,
где m — масса маховика; R
— его
радиус. Тогда формула (1) примет вид mR2
n.
Момент
инерции маховика J=mR2,
где m — масса маховика; R
— его
радиус. Тогда формула (1) примет вид mR2![]() n
= M∆t, откуда
n
= M∆t, откуда

Угол поворота, т. е. угловой путь φ, за время вращения маховика до остановки может быть определен по формуле для равнозамедленного вращения: φ = ω0t—е∆t2/2, (2) где е - угловое ускорение. По условию задачи, ω = ω0—е∆t, ω =0, е∆t = ω 0. Тогда выражение (2) может быть записано так:
φ = ω0∆t— ω0∆t/2= ω0∆t/2 .
Так
как φ = ![]() n,
ω 0 =
n,
ω 0 = ![]() n,
то число полных оборотов
n,
то число полных оборотов
N= n∆t/2; N =12 c-1*30 с/2 = 180.
Ответ: М=1,61 Н*м, N=180.
КОНТРОЛЬНАЯ РАБОТА № 1
1(1). Под действием какой силы при прямолинейном движении тела изменение его координаты со временем происходит по закону x=10t—20t2? Масса тела 5 кг.
2(2). Найти закон движения тела массой m под действием постоянной силы F, если в момент t=0 тело покоилось в начале координат (x=0).
3(3). Найти закон движения тела массой m под действием постоянной силы F, если в момент t=0 начальная координата x=0 и v = v0.
4(4). Найти закон движения тела массой m под действием постоянной силы F, если в момент t=0 имеем x=х0 и v = v0.
5(5). Тело массой 2 кг движется с ускорением, изменяющимся по закону а = 5t-10. Определить силу, действующую на тело через 5 с после начала действия, и скорость в конце пятой секунды.
6(6). По условию предыдущей задачи определить силу, действующую на тело через 10 с после начала действия, и путь, пройденный телом за это время.
7(7). Под действием постоянной силы 10 Н тело движется прямолинейно и зависимость пройденного пути от времени имеет вид s=10-5t+2t2. Найти массу тела.
8(8). Зависимость пройденного телом пути от времени имеет вид s = 2t—3t2+4t3. Найти зависимость скорости от времени и силу, действующую на тело в конце второй секунды. Масса тела 1 кг.
9(9). По условию предыдущей задачи найти зависимость ускорения от времени. Определить, в какой момент времени сила, действующая на тело, равна нулю.
10(10). Тело массой 2 кг движется прямолинейно со скоростью, зависимость которой от времени выражается уравнением v = 2,5t2 + 10t. Определить путь, пройденный телом за 5 с, и силу, действующего на тело в конце пятой секунды.
11(11). Прямоугольный брусок размером 3,3X3,3X6,9 см движется параллельно большому ребру. При какой скорости движения он будет казаться кубом?
12(12). Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились в два раза?
13(13). При какой относительной скорости движения релятивистское сокращение длины движущегося тела составит 50 %?
14(14). π-мезон нестабильная частица. Собственное время жизни его 2,6*10-8 с. Какое расстояние пролетит π-мезон до распада, если он движется со скоростью 0,99 с?
15(15). По условию предыдущей задачи определить, на сколько расстояние, пролетаемое π-мезоном, при релятивистском замедлении времени больше, чем если бы такого замедления не было.
16(16). Найти собственное время жизни нестабильной частицы μ-мезона, движущегося со скоростью 0,99 с, если расстояние, пролетаемое им до распада, равно примерно 10 км.
17(17). Собственное время жизни π-мезона 2,6-10-8 с. Чему равно время жизни π-мезона для наблюдателя, относительно которого эта частица движется со скоростью 0,95 с?
18(18). Электрон, скорость которого 0,97 с, движется навстречу протону, имеющему скорость 0,5 с. Определить скорость их относительного движения.
19(19). Радиоактивное ядро вылетевшее из ускорителя со скоростью 0,4 с, выбросило в направлении своего движения β-частицу со скоростью 0,75 с относительно ускорителя. Найти скорость частицы относительно ядра.
20(20). Скорость света в стоячей воде и = с/п, где с — скорости света в вакууме; п — показатель преломления воды. Найти скорость света в воде, движущейся равномерно относительно источника света со скоростью v.
21.Вывести формулу, по которой вычисляется кинетическая энергия тела массой m, движущегося под действием постоянной силы F, если t= 0, v0=0.
22.Скорости двух центрально соударяющихся шаров до их взаимодействия равны 0,1 и 0,05 м/с, их массы соответственно равны 4 и 3 кг. Определить их скорости после удара при упругом coударении.
23.В каком случае двигатель автомобиля совершит большую работу (во сколько раз): для разгона с места до скорости 36 км/ч или при увеличении скорости от 36 до 72 км/ч. Силу сопротивления и время движения в обоих случаях считать одинаковыми.
24.Шар массой 4 кг движется со скоростью 2 м/с и сталкивается с покоящимся шаром массой 1 кг. Вычислить работу, совершенную вследствие деформации шаров при прямом центральном ударе. Шары считать неупругими.
25.Тепловоз массой 40 т, двигаясь со скоростью 1 м/с, ударяется в два неподвижных пружинных буфера вагона. Найти наибольшее сжатие буферов вагона, если коэффициент упругости пружины 5*106 Н/м, и продолжительность удара.
26.Для того чтобы растянуть пружину на длину х, требуется приложить силу F=kx. Какая работа совершается при растяжении пружины на длину х1? Потенциальная энергия деформированной пружины П=Ах12. Найти силу, действующую на пружину.
27.На тело действует сила F=kx2. На сколько увеличится потенциальная энергия тела при его перемещении из точки х=0 в1 точку x=х1?
28.Стальная цепочка длиной 1 м, лежащая на столе, начинает скользить, если 0,15 м этой цепочки спущены со стола. Масса цепочки 3 кг, коэффициент трения между столом и цепочкой 0,1. Какая работа против сил трения совершается при соскальзывании всей цепочки?
29.Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени выражается уравнением s = t2+2t +2. Определить работу силы за 5 с после начала ее действия.
30.По условию предыдущей задачи найти зависимость кинетической энергии от времени и пути.
31.Масса движущегося протона 2,25*10-27 кг. Найти скорость и кинетическую энергию протона.
32.Электрон прошел ускоряющую разность потенциалов в 100 MB. Во сколько раз его релятивистская масса больше массы покоя? Чему равна скорость электрона?
33.Определить скорость протона, если его релятивистская масса в три раза больше массы покоя. Вычислить кинетическую и полную энергию.
34.Вычислить скорость, полную и кинетическую энергию протона в тот момент, когда его масса равна массе α-частицы.
35.Найти импульс, полную и кинетическую энергию электрона, движущегося со скоростью, равной 0,7 с.
36.Протон и α-частица проходят одинаковую ускоряющую разность потенциалов, после чего масса протона составила половину массы α-частицы. Определить разность потенциалов.
37.Определить соотношение между полной энергией E, энергией покоя Е0 и импульсом р релятивистской частицы.
38.Вывести соотношение между полной энергией, массой покоя и импульсом релятивистской частицы.
39.С какой скоростью движется электрон, если его кинетическая энергия 1,78 МэВ? Определить импульс электрона.
40.Кинетическая энергия частицы оказалась равной ее энергии покоя. Какова скорость этой частицы?
41.На каком расстоянии от центра Земли находится точка, в которой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и расстояние от центра Земли до центра Луны равно 60 радиусам Земли.
42.С какой скоростью упадет на поверхность Луны метеорит, скорость которого вдали от Луны мала? Атмосфера на Луне отсутствует.
43.Какую работу необходимо совершить, чтобы вывести тело массой 250 кг на орбиту искусственной планеты солнечной системы?
44.Определить работу, которую совершают силы гравитационного поля Земли, если тело массой 2 кг упадет на поверхность Земли с высоты, равной радиусу Земли.
45. По условию предыдущей задачи определить работу, совершаемую силами гравитационного поля Земли, если тело падает поверхность Земли из бесконечности.
46.Ракета была запущена с Земли с начальной скоростью 10 км/с. Определить скорость ракеты на орбите, предположив, что орбита круговая и ее радиус равен двум радиусам Земли. Сопротивление воздуха не учитывать.
47. Вычислить первую и вторую космические скорости тела, запущенного с Земли.
48. Вычислить первую и вторую космические скорости тела, запущенного с Луны.
49. На какой высоте над поверхностью Земли напряженность гравитационного поля — 0,5 Н/кг? Определить потенциал поля тяготения на этой высоте.
50. Как изменятся напряженность и потенциал гравитационного поля Земли на высоте, равной радиусу Земли? Принять ускорение свободного падения вблизи поверхности Земли равным 9,8 м/с2.
51. Материальная точка массой 1 г движется по окружности радиуса 2 м согласно уравнению s = 8t—0,2t3. Найти скорость, тангенциальное, нормальное и полное ускорения в момент времени 3 с
52. Тело вращается равноускоренно с начальной угловой скоростью 5 с-1 и угловым ускорением 1 с-2. Сколько оборотов сделает тело за 10 с?
53. Материальная точка движется по окружности радиусом 0,5 м. Ее тангенциальное ускорение 10 м/с2. Чему равны нормальное и полное ускорения в конце третьей секунды после начала движения. Найти угол между векторами полного и нормального ускорений в этот момент.
54. Колесо автомобиля, вращающегося с частотой 1200 мин при торможении стало вращаться равнозамедленно и остановилось через 20 с. Найти угловое ускорение и число оборотов с момент начала торможения до остановки.
55. Сплошной шар массой 1 кг и радиусам 5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара выражается уравнением φ=4 + 2t-t2. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.
56. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Закон движения автомобиля выражается уравнением s=10+10t—0,5t2. Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения в конце пятой секунды.
57. От самолета, летящего горизонтально со скоростью 500 м/с, оторвался предмет. Чему равны нормальное и тангенциальное ускорения предмета через 50 с после начала падения? Сопротивление воздуха не учитывать.
58.Тело брошено со скоростью 15 м/с под углом 30° к горизонту. Определить наибольшую высоту подъема, дальность полета, радиус кривизны траектории в наивысшей точке.
59.По условию предыдущей задачи определить скорость тела, а также его нормальное и тангенциальное ускорения через 2 с после начала движения.
60.Артериальная точка движется по окружности, диаметр которой 40 м. Зависимость пути, пройденного точкой, от времени выражается уравнением s = t3+4t2—t+8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3 с от начала ее движения.
61(21). Два горизонтально вращающихся один над другим диска расположены так, что плоскости их параллельны, а центры лежат на одной вертикали. Угловая скорость и момент инерции первого диска равны ω1 и J1 и а второго соответственно ω2 и J2. Первый диск падает на второй, и система вращается как единое целое. Определить угловую скорость вращающейся системы и изменение кинетической энергии дисков после падения первого на второй.
62(22). Сплошной цилиндр массой 10 кг катится без скольжения с постоянной скоростью 10 м/с. Определить кинетическую энергию цилиндра и время до его остановки, если на него действует сила трения 50 Н.
63(23). Сплошной шар скатывается по наклонной плоскости, длина которой 10 м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.
64(24). Полый цилиндр массой 2 кг катится по горизонтальной поверхности со скоростью 20 м/с. Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 1,6 м.
65(25). Маховик, имеющий форму диска массой 30 кг и радиусом 10 см, был раскручен до частоты 300 мин-1. Под действием силы трения диск остановился через 20 с. Найти момент сил трения, считая его постоянным.
66(26). Какой скоростью должен обладать шар, катящийся без скольжения, чтобы подняться по наклонной плоскости, составляющей с горизонтом угол 30°, на высоту 2 м, если сила трения равна 0,2 силы давления шара на плоскость? Чему равно время подъема?
67(27). По условию предыдущей задачи определить, с какой скоростью и в течение какого времени шар скатится обратно.
68(28). Сначала диск, а потом обруч скатываются с наклонной плоскости, составляющей угол α с горизонтом. Чему равны их ускорения? Силой трения пренебречь.
69(29). Шар и сплошной цилиндр имеют одинаковую массу 5 кг каждый и катятся с одинаковой скоростью 10 м/с. Найти кинетические энергии этих тел.
70(30). Стержень массой 2 кг и длиной 1 м может вращаться вокруг оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой 10 г, летящая перпендикулярно оси и стержню со скоростью 500 м/с. Определить угловую скорость, с которой начнет вращаться стержень, если пуля застрянет в нем.
II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
ПОЯСНЕНИЯ К РАБОЧЕЙ ПРОГРАММЕ
Приступая к изучению раздела «Основы молекулярной физики и термодинамики», студенты должны уяснить, что существуют два качественно различных и взаимодополняющих метода исследования физических свойств макроскопических систем — статистический (молекулярно-кинетический) и термодинамический. Молекулярно-кинетический метод исследования лежит в основе молекулярной физики, термодинамический — в основе термодинамики. Молекулярно-кинетическая теория является важнейшей теорией, которая позволяет с единой точки зрения рассмотреть самые различные явления во всех состояниях вещества, вскрыть физическую сущность этих явлений и теоретическим путем вывести многочисленные закономерности, открытые экспериментально и имеющие большое практическое значение.
При изучении молекулярно-кинетической теории следует уяснить, что свойства огромной совокупности молекул отличны от свойств каждой отдельной молекулы и свойства макроскопической системы и конечном счете определяются свойствами частиц системы, особенностями их движения и средними значениями кинематических характеристик частиц, т. е. их скоростей, энергий и т. д.
В отличие от молекулярно-кинетической теории термодинамика не изучает конкретно молекулярные взаимодействия, происходящие с отдельными атомами или молекулами, а рассматривает взаимопревращения и связь различных видов энергии, теплоты и работы. Термодинамика базируется на двух опытных законах (началах), которые позволяют описывать физические явления, связанные с превращением энергии макроскопическим путем.
При изучении основ термодинамики студент должен четко усвоить такие понятия, как термодинамическая система, термодинамические параметры (параметры состояния), равновесное состояние, I уравнение состояния, термодинамический процесс, внутренняя энергия, энтропия и т. д.
Контрольная работа № 2 построена таким образом, что она дает возможность проверить знания студентов по основным вопросам данного раздела.
В задачах на тему «Основы молекулярно-кинетической теории» внимание уделено таким вопросам программы, как уравнение Клапейрона-Менделеева, уравнение молекулярно-кинетической теории, средние кинетические энергии поступательного и вращательного движения молекул, средняя длина свободного пробега и среднее число соударений, явления переноса.
Задачи по теме «Основы термодинамики» охватывают такие важные соотношения и понятия, как первое начало термодинамики, внутренняя энергия, работа при различных изопроцессах и адиабатном процессе. Включены также задачи, которые позволяют изучить и понять такие вопросы, как второе начало термодинамики и энтропия идеального газа, являющаяся в отличие от количества теплоты
функцией состояния. В работе представлены задачи на определение
КПД цикла Карно, изменение энтропии, на уравнение Ван-дер-Ваальса, которое объясняет отличие свойств реальных газов от идеальных.
Основные законы и формулы:
Количество
вещества ![]()
Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа)
![]()
Закон
Дальтона ![]()
Концентрация молекул ![]()
Уравнение молекулярно-кинетической теории газов 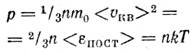
Средняя
кинетическая энергия молекулы ![]()
Внутренняя энергия идеального газа ![]()
Скорости молекул:
средняя квадратичная

средняя арифметическая ![]()
Средняя
длина свободного пробега молекулы 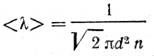
Среднее
число соударений молекулы за 1 с ![]()
Распределение молекул в потенциальном поле сил (распределение Вольцмана)
![]()
Барометрическая формула ![]()

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. В сосуде объемом 2 м3 находится смесь 4 кг гелия и 2 кг водорода температуре 27°С. Определить давление и молярную массу смеси газов.
Дано: V=2 м3, m1 = 4 кг, М1=4*10-3 кг/моль, m2=2 кг, М2=2*10-9 кг/моль, Т=300 К.
Найти: Р, М.
Решение. Воспользуемся, уравнением Клапейрона—Менделеева, применив его к гелию и водороду:
p1V =m1RT/M1 (1) , p2V =m2RT/M2 (2)
где p1 - парциальное давление гелия; m1 — масса гелия; M1 — его
молярная масса; V — объем сосуда; Т — температура газа; R =
8.31 Дж/(моль*К)—молярная газовая постоянная; р2—парциальное водорода; m2—масса водорода; М2— его молярная масса. Под парциальным давлением p1 и p2 понимается то давление, которое производил бы газ, если бы он только один находился в сосуде. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси: р=р1+р2. Из уравнений (1) и (2) выразим р1 и р2 и подставим в уравнение (3):
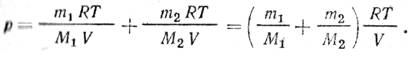
Найдем молярную массу смеси газов по формуле M=(m1+m2)/( v1+v2) (5) где v1 и v2 — число молей гелия и водорода соответственно. Число молей газов найдем по формулам:. v1=m1/M1 (6) , v2=m2/M2 (7). Подставляя (6) и (7) в (5), найдем:
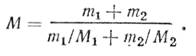
Подставляя числовые значения в формулы (4) и (8), получаем:

Ответ: р=2493 кПа, M=3*10-3 кг/моль.
2. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 2 кг водорода при температуре 400 К?
Дано: m = 2 кг, T=400 К, M=2*10-3 кг/моль.
Найти: <eпост>, <eвр>.
Решение. Считаем водород идеальным газом. Молекула водорода — двухатомная, связь между атомами считаем жесткой, тогда число степеней свободы молекулы водорода равно 5. В среднем на одну степень свободы приходится энергия <ei>=kT/2, где k— постоянная Больцмана; Т — термодинамическая температура. Поступательному движению приписывается три (i=3), а вращательному две (i=2) степени свободы. Тогда энергия одной молекулы
<eпост> = 3/2кТ, <евр> = 2/2 kТ.
Число молекул, содержащихся в массе газа, N=vNA =(m/M)NA где v —число молей; NА — постоянная Авогадро. Тогда средняя кинетическая энергия поступательного движения молекул водорода будет
<eпост> =(m/M)NA *3/2 kT = 3/2 (m/M)RT, (1)
где R=kNА —молярная газовая постоянная.
Средняя кинетическая энергия вращательного движения молекул водорода
<eвр> = (m/M) RT. (2)
Подставляя числовые
значения в формулы (1) и (2), имеем

Ответ: <eпост> = 4986 кДж, <евр>=2324 кДж.
3. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 27 oС и давлении 100 кПа.
Дано: V = 2л=2*10-3 м3, M=32*10-3 кг/моль, Т=300 К, p = 100 кПа=105 Па, в=2,9*10-10 м.
Найти: <λ>,Z .
Решение. Средняя длина свободного пробега молекул кислорода вычисляется по формуле < λ > = l/(21/2*πd2n), (1) где d— эффективный диаметр молекулы кислорода; п — число молекул в единице объема, которое можно определить из уравнения p=nkT, откуда n=p/(kT), (2) где k — постоянная Больцмана. Подставляя (2) в (1), имеем
< λ > = kT/(21/2*πd2p) (3)
Число соударений Z, происходящих между всеми молекулами за 1 с равно
Z = ½<Z> N (4)
где N - число молекул кислорода в сосуде объемом 2*10-3 м3;
<Z> - среднее число соударений одной молекулы за 1 с. Число молекул в сосуде N=nV. (5). Среднее число соударений молекулы за 1 с равно <Z> = <v>/< λ >, (6) где <v> — средняя арифметическая скорость молекулы <v>=(8RT/πM). (7)
Подставляя в (4) выражения (5), (6) и (7), находим

Подставляя числовые значения, получим

Ответ: Z=9*1028 c-1, < λ > = 3,56*10-8м.
4. Определить коэффициенты диффузии и внутреннего трения азота, находящегося при температуре Т=300 К и давлении 105 Па.
Дано: po=1,25 кг/м3, M=28*10-3 кг/моль, Т=300 К, р=105 Па, d=3,1*10-1 м.
Найти: D, η.
Решение . Коэффициент диффузии определяется по формуле
D=1/3 <v> <λ> ,
где <v> - средняя арифметическая скорость молекул, равная <v> = (8RT/(πM))1/2 (2) <λ> — средняя длина свободного пробега молекул. Для нахождения <λ> воспользуемся формулой, взятой из решения примера 3: < λ >=kT/(21/2*πd2p). (3) Подставляя (2) и (3) в выражение (1), имеем (4)
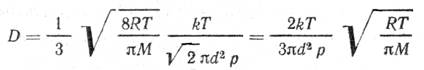
Коэффициент внутреннего трения
η = 1/з<v>< λ >р, (5)
где p — плотность газа при температуре 300 К и давлении 105 Па, Для нахождения р воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота — при нормальных условиях (Tо = 273 К, р=1,01*105 Па) и условиях задачи:
p0V0 = (m/M)RT0, pV = (mlM) RT . (6)
Учитывая, что po=m/V0, p = m/V, имеем р=рорТо/(роТ), (7)
Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии [см. (1) и (5)]:
η = Dp = Dp0pT0/(p0T). (8)
Подставляя числовые значения в (4) и (8), получим
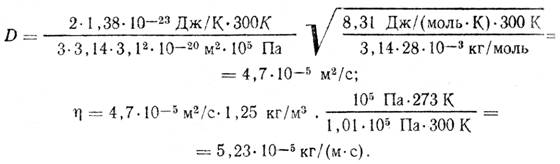
Ответ: D=4,7-10-5 м2/с, т] = 5,23-10-3 кг/(м-с). .
5. Кислород массой 160 г нагревают при постоянном давлении от 320 до 340 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа.
Дано: m=160 г=16*10-2 кг,Т1=320 К, Т2=340 К.
Найти: Q, ∆U, А.
Решение. Количество теплоты, необходимое для нагревания газа при постоянном давлении,
Q = mcp (Т2 - Tt) = (m/M) Ср (Т2 – T1) . (1)
Здесь ср и Ср=Мср — удельная и молярная теплоемкости газа при постоянном давлении; М=32*10-3 кг/моль — молярная масса кислорода. Для всех двухатомных газов
Ср = 7/2R; Ср = 3,5*8,31 Дж/(моль*К) = 29 Дж/(моль*К).
Изменение внутренней энергии газа находим по формуле ∆U =(m/М)Сv/(T2-T1),
где Cv—молярная теплоемкость газа при постоянном объеме. Для всех двухатомных газов
Cv = 5/2 R; Сv = 2,5*8,31 Дж/(моль*К) = 20,8 Дж/(моль*К).
Работа расширения газа при изобарном процессе A = р∆V, где ∆V=V2-V1— изменение объема газа, которое можно найти из уравнения Клапейрона-Менделеева. При изобарном процессе
pV1 = (m/M)RT1, (3) pV2 = (m/M)RT2. (4)
Почленным вычитанием выражения (4) из (3) находим
p(V2-V1) = (m/M)R(T2-T1),
следовательно,
A = (m/M)R(T2-T1) (5)
Подставляя числовые значения в формулы (1), (2) и (5), получаем:
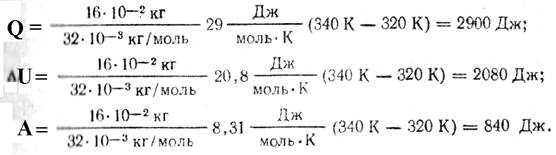
Ответ: Q=2900 Дж, ∆U = 2080 Дж, A=840 Дж.
6. Объем аргона, находящегося при давлении 80 кПа, увеличился от 1 до 2 л. Па сколько изменится внутренняя энергия газа, если расширение производилось: а) изобарно; б) адиабатно.
Дано: V1= 10-3 м3, V2=2*10-3 м3, p=0,8*105 Па, М=40*10-3 кг/моль, i = 3.
Найти ∆U.
Решение. Применим первый закон термодинамики. Согласно этому закону количество теплоты Q, переданное системе, расходуется на увеличение внутренней энергий ∆U и на внешнюю механическую работу A:Q=∆U+A. (1) Величину ∆U можно определить, зная массу газа m, удельную теплоемкость при постоянном объеме Cv и изменение температуры ∆T: ∆U =mcv∆T. (2) Однако удобнее изменение внутренней энергии ∆U определять через молярную теплоемкость Cv , которая может быть выражена через число степеней свободы: Cv= Cv/M=1/2 R/M . (3) Подставляя величину Cv из формулы (3) в (2), получаем
∆U = (m/M)*(i/2)* R∆T. (4)
|
(2) |
Изменение внутренней энергии зависит от характера процесса, при котором идет расширение газа. При изобарном расширении газа согласно первому закону термодинамики часть количества теплоты идет на изменение внутренней энергии ∆U , которая выражается формулой (4). Найти ∆U для аргона по формуле (4) нельзя, так как масса газа и температура в условии задачи не даны. Поэтому необходимо провести преобразование формулы (4).
Запишем уравнение Клапейрона-Менделеева для начального и конечного состояний газа:
pV1=(m/M)RT1 и pV2 = (m/M) RT2,
или
p(V2-V1)=(m/M)R(T2-T1)
Подставив (5) в формулу (4), получим
∆U= (i/2)p(V2-V1) .
Это уравнение является расчетным для определения ∆U при изобарном расширении.
При адиабатном расширении газа теплообмена с внешней средой не происходит, поэтому Q=0. Уравнение (1) запишется в виде ∆U+A=0. (7) Это соотношение устанавливает, что работа расширения газа может быть произведена только за счет уменьшения внутренней энергии газа (знак минус перед ∆U):
А=— ∆U. (8)
Формула работы для адиабатного процесса имеет вид
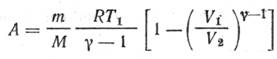
где γ— показатель степени адиабаты, равный отношению теплоемкостей: γ = Cp/Сv=(i+2)/i. Для аргона — одноатомного газа (i=3) имеем γ = 1,67.
Находим изменение внутренней энергии при адиабатном процессе для аргона, учитывая формулы (8) и (9):
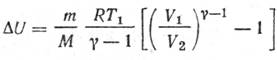
Для определения работы расширения аргона формулу (10) следует преобразовать, учитывая при этом параметры, данные в условии задачи. Применив уравнение Клапейрона—Менделеева для данного случая p1V1 = (m/M)RT1 , получим выражение для подсчета изменения внутренней энергии:
![]()
Подставляя числовые значения в (6) и (11), получим
a) при изобарном расширении
∆U=3\2*0,8*105Па*10-3 м3= 121 Дж
б) при адиабатном расширении

Ответ: a) ∆U=121 Дж ; б) ∆U=-44,6 Дж.
7. Температура нагревателя тепловой машины 500 К. Температура холодильника 400 К. Определить КПД тепловой машины, работающей по циклу Карно, и полную мощность машины, если нагреватель ежесекундно передает ей 1675 Дж теплоты. Дано: Т=500 К, Т0=400 К, Q=1675 Дж.
Найти: η, N.
Решение: КПД машины определяется по формуле:
η = (T-T0)/T (1) или η=A/Q (2)
Из выражений (2) и (1) находим
A= η Q=(T-T0)/T .
Произведем вычисления:
Η = (500К-400К)/500К = 0,2 ;
A=0,2*1675 Дж = 335 Дж .
Этаработа совершается за 1 с, следовательно, полная мощь машины 335 Вт.
Ответ: η=0.2, N=335Вт.
8. Горячая вода некоторой массы отдает теплоту холодной воде такой же массы и температуры их становятся одинаковыми. Показать, что энтропия при этом увеличивается.
Решение: пусть температура горячей воды T1, холодной Т2, а температура смеси θ. Определим температуру смеси, исходя из уравнения теплового баланса
mc (T2- θ)= mc (θ- T2), или Т1- θ= θ-Т2,
откуда θ=(Т1+Т2)/2 . (1)
Изменение энтропии, происходящее при охлаждении горячей воды,
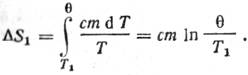
Изменение энтропии, происходящее при нагревании холодной воды,
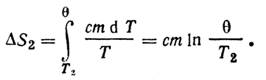
Изменение энтропии системы равно
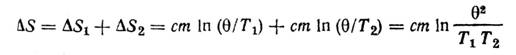
или с учетом соотношения (1) имеем
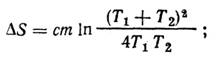
так как (Т1+Т2)2>4T1T2, то ∆S>0.
9. Вычислить эффективный диаметр молекул азота, если его критическая температура 126 К, критическое давление 3,4 МПа.
Дано: Ткр = 126 К, ркр = 3,4 *106 Па.
Найти d.
Решение. Азот, согласно условию задачи, должен подчиняться уравнению Ван-дер-Ваальса:
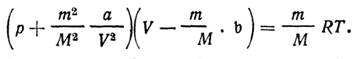
Постоянную b в уравнении Ван-дер-Ваальса с достаточной степенью точности считают равной учетверенному собственному объему 1 моля газа. В 1 моле газа находится 6,02*1023 молекул (NA = 6,02*1023 моль-1), следовательно, объем одной молекулы равен
![]()
Откуда
![]()
Постоянная b = Tкp R /(8pкр), тогда
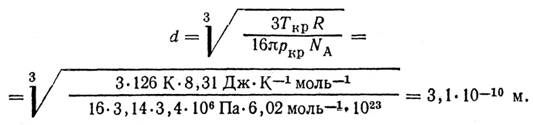
Ответ: d=3,1*10-10 м.
КОНТРОЛЬНАЯ РАБОТА № 2
1. В баллоне емкостью 0,5 м3 находится 4 кг водорода и 6,5 кг азота. Определить давление смеси, если температура окружающей среды 18оС.
2. В баллоне емкостью 30 л находится сжатый воздух при 17 °С. После того как часть воздуха выпустили, давление понизилось на 2*105 Па. Определить массу выпущенного воздуха. Процесс считать изотермическим.
3. В сосуде, имеющем форму шара, радиус которого 0,2 м, находится 80 г азота. До какой температуры можно нагреть сосуд, если его стенки выдерживают давление 7*105 Па?
4. При какой температуре находится газ, если при нагревании его на 20° при постоянном давлении объем увеличился в два раза? Для каких газов это возможно?
5. В баллоне под давлением 1 МПа находится газовая смесь из кислорода и азота. Считая, что масса азота составляет 80 % от массы смеси, определить парциальное давление отдельных газов.
6. Определить молекулярную формулу аммиака, если при давлении 103 740 Па и температуре 20 °С его плотность равна 0,736 кг/м3. Учесть, что элементы, из которых образуется аммиак, — это азот и водород.
7. До какой температуры нужно нагреть запаянный шар, содержащий 35 г воды, чтобы шар разорвался, если известно, что стенки шара выдерживают давление 2*107 Па, Объем шара 1 л.
8. В пустой сосуд, объем которого 5 дм3, впустили 3дм3 азота под давлением 250 кПа и 4 дм3 водорода под давлением 50 кПа. Каково давление образовавшейся смеси?
9. Какой объем при нормальных условиях занимает смесь 4 кг кислорода и 2 кг азота?
10. При температуре 27 °С и давлении 12*105 Па плотность смеси водорода и азота 10 г/дм3. Определить молярную массу смеси.
11(31). Определить среднюю кинетическую энергию вращательного движения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа 6,02 МДж.
12(32). Сколько молекул водорода находится в сосуде емкостью 2 л, если средняя квадратичная скорость движения молекул 500 м/с, а давление на стенки сосуда 103 Па?
13(33). Найти среднюю кинетическую энергию вращательного движения всех молекул, содержащихся в 0,25 г водорода при температуре 13 °С.
14(34). Давление идеального газа 2 мПа, концентрация молекул 2*1010 см-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.
15(35). Определить среднее значение полной кинетической энергии одной молекулы неона, кислорода и водяного пара при температуре 600 К.
16(36). Средняя кинетическая энергия поступательного движения молекул газа равна 5-10-21 Дж. Концентрация молекул 3*1019 см-3. Определить давление газа.
17(37). В сосуде емкостью 200 см3 находится газ при температуре 47оС. Из-за утечки газа из колбы просочилось 1021 молекул. Haсколько снизилось давление газа в сосуде?
18(38). Сколько молекул газа находится в сосуде емкостью 1,5 л при нормальных условиях?
19(39). Определить концентрацию молекул идеального газа при температуре 450 К и давлении 1,5 МПа.
20(40). Определить температуру идеального газа, если средняя кинетическая энергия поступательного движения его молекул 3,2*10 -19 Дж.
21.В сосуде емкостью 10 л находится 2 г кислорода. Опреде-1 лить среднюю длину свободного пробега молекул.
22.Определить среднюю длину свободного пробега молекул азота, если плотность разреженного газа 0,9-10-6 кг/м3.
23.При каком давлении средняя длина свободного пробега молекул кислорода равна 1,25 м, если температура газа 50 °С?
24.Вычислить среднюю длину свободного пробега молекул воздуха при давлении 1*105 Па и температуре 10 °С.
25.По условию предыдущей задачи вычислить коэффициент диффузии воздуха.
26.Во сколько раз коэффициент диффузии молекул водорода больше коэффициента диффузии молекул азота? Температура и давление газов одинаковые.
27.Сколько соударений в секунду в среднем испытывают молекулы азота, находящиеся при нормальных условиях?
28.Определить коэффициент внутреннего трения углекислого газа при температуре 300 К.
29.Сосуд емкостью 10 л содержит водород массой 4 г. Определить среднее число соударений молекул в секунду.
30.Коэффициент внутреннего трения кислорода при нормальных условиях 1,91*10-4 кг/(м*с). Какова средняя длина свободного пробега молекул кислорода при этих условиях?
31(41). При нагревании 1 кмоля азота было передано 1000 Дж теплоты. Определить работу расширения при постоянном давлении.
32(42). Определить, какое количество теплоты необходимо сообщить углекислому газу массой 220 г, чтобы нагреть его на 20 К: а) при постоянном объеме; б) при постоянном давлении.
33(43). Какое количество теплоты нужно сообщить 1 кмолю кислорода, чтобы он совершил работу в 1000 Дж: а) при изотермическом процессе; б) при изобарном?
34(44). Азот массой 2 кг, находящийся при температуре 288 К, сжимают: а) изотермически; б) адиабатно, увеличивая давление 10 раз. Определить работу, затраченную на сжатие газа, в обоих случаях.
35(45). При каком процессе выгоднее производить расширение углекислого газа: адиабатном или изотермическом, если объем увеличивается в 2 раза? Начальная температура в обоих случаях одинаковая.
36(46). Найти работу и изменение внутренней энергии при адиабатном расширении 1 кг воздуха, если его объем увеличился в 10 раз. Начальная температура 15 °С.
37(47). Определить количество теплоты, сообщенное 20 г азота, если он был нагрет от 27 до 177 °С. Какую работу при этом совершит газ и как изменится его внутренняя энергия?
38(48). Во сколько раз увеличится объем 1 моля водорода при изотермическом расширении при температуре 27 °С, если при этом была затрачена теплота, равная 4 кДж.
39(49). Водород, занимающий объем 5 л и находящийся под давлением 105 Па, адиабатно сжат до объема 1 л. Найти работу сжатия и изменение внутренней энергии водорода.
40(50). Газ, занимающий объем 20 л под давлением 1 МПа, был изобарно нагрет от 323 до 473 К. Найти работу расширения газа.
41.Тепловая машина работает по циклу Карно, КПД которого 0,2. Каков будет КПД этой машины, если она будет совершать тот же цикл в обратном направлении?
42.Холодильная машина работает по обратному циклу Карно, КПД которого 300 %. Каков будет КПД тепловой машины, работающей по прямому циклу Карно?
43.Определить работу идеальной тепловой машины за один цикл, если она в течение цикла получает от нагревателя количество теплоты 2095 Дж. Температура нагревателя 500 К, холодильника 300 К.
44.Температура нагревателя тепловой машины, работающей по циклу Карно, 480 К, температура холодильника 390 К. Какова должна быть температура нагревателя при неизменной температуре холодильника, чтобы КПД машины увеличился в 2 раза?
45.За счет 1 кДж теплоты, получаемого от нагревателя, машина, работающая по циклу Карно, совершает работу 0,5 кДж. Температура нагревателя 500 К. Определить температуру холодильника.
46.При прямом цикле Карно тепловая машина совершает работу 200 Дж. Температура нагревателя 375 К, холодильника 300 К. Определить количество теплоты, получаемое машиной от нагревателя.
47. Определить, на сколько процентов изменится КПД прямого цикла Карно, если температура нагревателя 894 К, а температура холодильника уменьшилась от 494 до 394 К.
48. Совершая прямой цикл Карно, газ отдал холодильнику 0,25 теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 500 К.
49.Какая часть теплоты, полученной от нагревателя, отдается холодильнику при прямом цикле Карно, если температура нагревав теля 500 К, температура холодильника 125 К?
50. Найти КПД цикла, состоящего из двух изобар и двух адиабат, если температуры характерных точек равны Т1 = 370 К, T2= 600 К, Т3 = 500 К, Т4=350 К. Решение пояснить диаграммой p-V.
51(51). Определить изменение энтропии 4 кг свинца при охлаждении его от 327 до 0° С.
52(52). Найти изменение энтропии при нагревании 1 кг воды от 0 до 100 °С и последующем превращении ее в пар при той же температуре.
53(53). Как изменится энтропия при изотермическом расширение 0,1 кг кислорода, если при этом объем его изменится от 2,5 до 10 л?
54(54). Определить изменение энтропии при изобарном нагревании 0,1 кг азота от 17 до 100°С.
55(55). Лед массой 100 г, находящийся при температуре —30 °С, превращается в пар. Определить изменение энтропии при этом.
56(56). Железо массой 1 кг при температуре 100 °С находится в тепловом контакте с таким же куском железа при 0°С. Чему будет равно изменение энтропии при достижении равновесной температуры 50 оС? Считать, что молярная теплоемкость железа равна 25,14 Дж/К.
57(57). Водород массой 10 г изобарно расширяется, при этом объем его увеличивается в 2 раза. Определить изменение энтропии водорода при этом процессе.
58(58). Определить изменение энтропии, происходящее при смешивании 5 кг воды, находящейся при температуре 280 К и 8 кг воды, находящейся при температуре 350 К.
59(59). Объем гелия, масса которого 2 кг, увеличился в 5 раз: а) изотермически, б) адиабатно. Каково изменение энтропии в этих случаях?
60(60). Определить изменение энтропии 1 моля идеального газа при изохорном, изобарном и изотермическом процессах.
61.Поправки для воды в уравнении Ван-дер-Ваальса равны а=0,566 Н*м4/моль2, b=3,06*10-5 м3/моль. Определить критический объем для 1 кг воды.
62.По условию задачи 61 определить значения критического давления и критической температуры.
63.Вычислить постоянные в уравнении Ван-дер-Ваальса для азота, если его критическая температура 126 К, а критическое давление 3383 кПа.
64.Найти критические параметры неона, если его постоянные в уравнении Ван-дер-Ваальса а = 0,209 Н-м4/моль2, b=1,7*10-5 м3/моль.
65.Азот массой 14 кг занимает объем 0,5 м3 при температуре 0°С. Пользуясь уравнением Ван-дер-Ваальса, найти на сколько нужно изменить температуру газа, чтобы его давление увеличилось вдвое.
66.В сосуде, объем которого 10 л, находится 360 г водяного пара при температуре 470 К. Вычислить давление пара, используя уравнение Ван-дер-Ваальса.
67.По условию задачи 66 определить внутреннее давление водяного пара и собственный объем молекул пара.
68.Определить эффективный диаметр молекулы газа, для которого критическая температура равна 282,7 К, поправка в уравнении Ван-дер-Ваальса a=45,3*10-2 Н*м4/моль2.
69.По уравнению Ван-дер-Ваальса определить давление, под которым находится 1 кмоль азота в сосуде объемом 2,5 м3, если его температура 310 К.
70.Найти постоянные в уравнении Ван-дер-Ваальса для углекислого газа, если критическая температура 304 К, а критическое давление 7370 кПа.