|
Теория пределов
I. Какая функция называется бесконечно малой?
a). 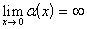 ; ;
b). 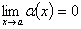 ; ;
c). 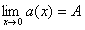 . .
II. Произведение бесконечно малой на ограниченную функцию есть ...
a). бесконечно малая функция;
b). ограниченная функция;
c). постоянная.
III. Число А называется пределом функции y=f(x) при x, стремящемся к а, если для любого числа
ε>0 существует такое δ>0, что при всех x, удовлетворяющих условию 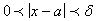 , выполняется неравенство , выполняется неравенство
a). 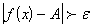 ; ;
b). 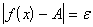 ; ;
c). 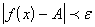 . .
IV. Если функция 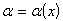 стремится к нулю при стремится к нулю при 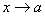 , то функция , то функция 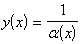 стремится к ... стремится к ...
a). бесконечности;
b). нулю;
c). единице .
V. Функция y=y(x) при 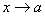
a). может иметь более
одного предела;
b). имеет пределы;
c). не может иметь более
одного предела.
VI. Функция y=f(x), определенная на интервале (a,b) , называется непрерывной в точке 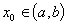 , если , если
a). 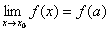 ; ;
b). 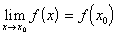 ; ;
c). 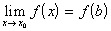 . .
VII. Если 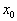 - точка разрыва первого рода функции f(x) , то - точка разрыва первого рода функции f(x) , то
a). конечные пределы
существуют и равны значению функции в этой точке;
b). конечные пределы
существуют;
c). конечные пределы равны.
VIII. Вычислить предел 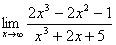
a). 2;
b). 0;
c). 0.5
IX. Бесконечно малая функция 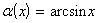 эквивалентна функции эквивалентна функции
a). 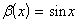 ; ;
b). 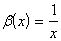 ; ;
c). 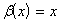 . .
X. Предел 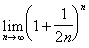 равен равен
a). е;
b). 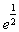 ; ;
c). 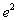 . . |